Elméleti áttekintés
Folytonos jelek esetében beszélünk folytonos konvolúcióról. Ha időtartományban vizsgálódunk akkor egy adott
folytonos idejű rendszer bemenő jele: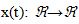 
és az impulzus-válaszfüggvénye h(t):
.
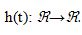Ekkor az LTI rendszer válasza az alábbi módon számolható ki:
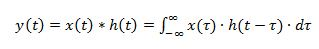
ahol * a konvolúciós szorzat (operátor) és konvolúciós integrálról beszélünk. A konvolúció feltétele, hogy az x(t) és h(t) közül legalább az egyik korlátos, a másiknak meg abszolút integrálhatónak kell lennie.
Alkalmazás használata:
Új függvény bemeneti az egér bal gombjának lenyomásával, illetve annak tartásával történik. Ha létrehoztuk a beviteli és az imuplzus-válaszfüggvényt, akkor a csúszka jobbra és balra húzásával rajzolódik ki a jel. Előtte célszerű normalizálni az impulzus-válaszfüggvényt.