Mérföldkövek
3. Mérföldkő
1. Kezelőfelület megvalósítás:
Kezelőfelület implementációja.
Létrehoztunk egy kezelőfelületet az alkalmazáshoz, mely az általunk készített tesztképekre illeszkedik:
Bemenetként egy rugót ábrázoló képet vár, amin referencia milliméterpapír található
Ki kell jelölni a rugót ábrázoló részt
Meg kell adni négy sarokpontot a milliméterpapíron
Be kell vinni a Matlab parancssorán keresztül a kijelölt milliméterpapír területen az x és y tengelyen lévő négyzetek számát, valamint egy négyzet méretét mm-ben
Ezután elkezdheti futását a program többi része a megfelelő képeken
2. Algoritmus megvalósítása:
Algoritmus megvalósítása.
A rugó sarokpontjait az alpha shape kerületi pontjait klaszterezve határozzuk meg. Ahhoz, hogy egy klaszterezett pontot felvegyünk a rugót leíró gráfba meg kell felelnie három kritériumnak:
Illeszkedjen az elotte lévő pontok által meghatározott egyenesre
Nagyjából azonos távolságra legyen az utolsó ponttól, mint az elotte lévo sarokpont
Fázisban is passzoljon a szemközti szakaszhoz
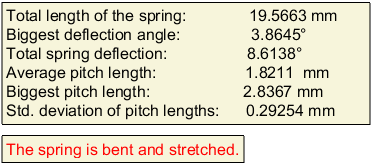
Mérőszámok.
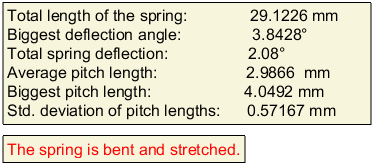
A teljes rugó hossza
Legnagyobb elhajlási szög értéke és helye
Rugó teljes ferdülése
Átlagos menetemelkedés
Legnagyobb menetemelkedés értéke és helye
Menetemelkedés szórása
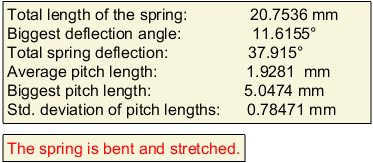
A teljes rugó hossza
Legnagyobb elhajlási szög értéke és helye
Rugó teljes ferdülése
Átlagos menetemelkedés
Legnagyobb menetemelkedés értéke és helye
Menetemelkedés szórása
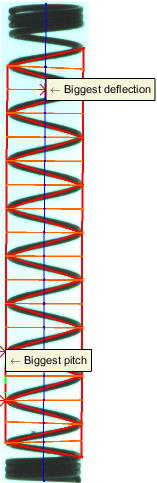
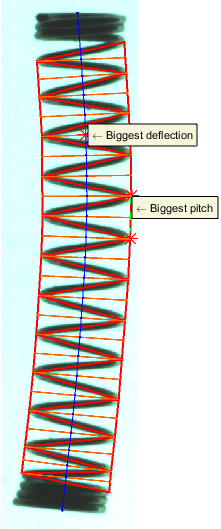
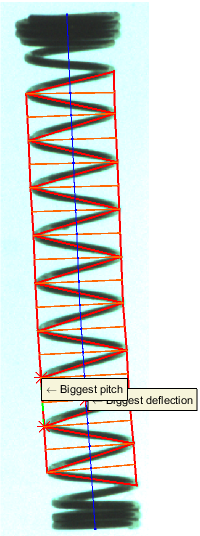
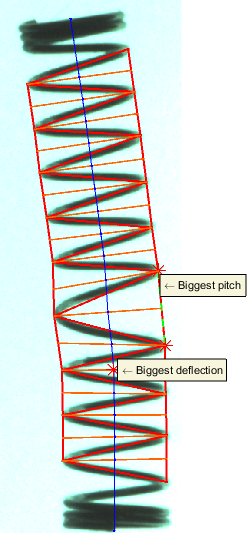
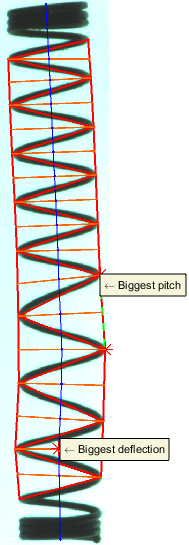
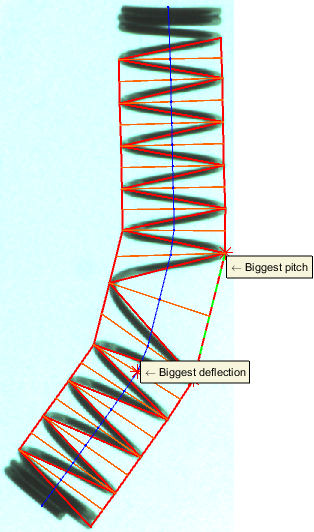
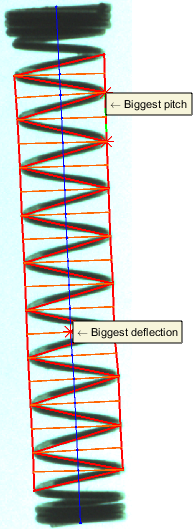
A teljes hossz kiszámolásához elobb a rugó tengelyvonalára van szükség. Ennek meghatározásához eloször a sarokpontok és a szemközti oldal felezopontjainak kiszámítására van szükség. A tengelyvonal ezen két pont felezoegyenese lesz, a teljes hossz pedig ezen felezoegyenesek hosszainak az összege. Az elso és az utolsó felezoegyenes meg van hosszabbítva, hogy kiérjen a rugó tetejére és aljára. Az ábrán kék színnel vannak jelölve a felezoegyenesek.
A legnagyobb elhajlási szög számítása a felezoegyenesek közötti elhajlások maximuma, a rugó ferdülése pedig ezen szögek összege. A legnagyobb elhajlás helye és értéke fel van tüntetve az eredményképeken.
A rugó emelkedésén a sarokpontokat összeköto szakaszok hosszát értjük. Kiszámoljuk a szakaszok számtani közepét (átlagos menetemelkedés), szórását, valamint maximumát és ennek helyét, melyek külön is fel vannak tüntetve az eredményképen.
3. Elért eredmények: